Implémentation de l’algorithme de tri à bulles en COBOL

Un des algorithmes de tri les plus simples à appréhender est celui du tri à bulles. Il consiste à balayer la liste autant de fois qu’il y a d’éléments, et à chaque passage de faire remonter en fin de liste les plus grands éléments détectés. C’est également l’algorithme le plus lent.

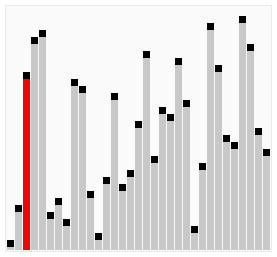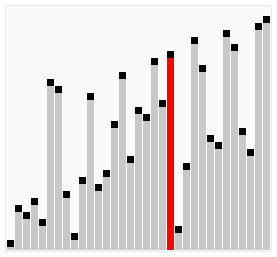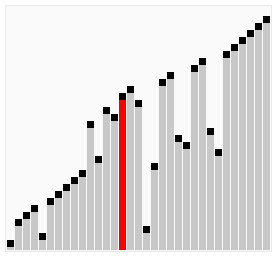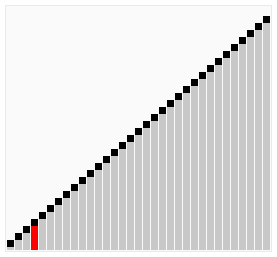
Explication animée du fonctionnement de l'algorithme de tri à bulles
Fonctionnement de l’algorithme de tri à bulles

Je vous propose une implémentation qui comporte des exemples d’utilisation des instructions COBOL suivantes :

Tableaux à taille dynamique : OCCURS … DEPENDING ON…
Boucles avec test à la fin : PERFORM WITH TEST AFTER
Double boucle imbriquée faisant varier deux indices : PERFORM VARYING … AFTER …

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

******************************************************************
* Component : BBUBSORT (COBOL batch)
* Author : Cyril Coquilleau
* Date : 2018-04-14
* Purpose : Implements bubble sort algorithm
******************************************************************
IDENTIFICATION DIVISION.
PROGRAM-ID. BBUBSORT.
DATA DIVISION.
WORKING-STORAGE SECTION.
*Array definition
01 ARRAY-SIZE PIC 9(9) VALUE 10000.
01 ELT-ARRAY OCCURS 0 TO 9999999 DEPENDING ON ARRAY-SIZE.
03 ELT-VALUE PIC 9(8).

*Indexes
01 POS PIC 9(9).
01 I PIC 9(9).
01 J PIC 9(9).
01 J-PLUS1 PIC 9(9).

*Temporary data for swapping
01 ELT-VALUE-TEMP PIC 9(8).

PROCEDURE DIVISION.

MAIN-PROCEDURE.
PERFORM VARYING POS FROM 1 BY 1 UNTIL POS > ARRAY-SIZE
COMPUTE ELT-VALUE(POS) = 1 + FUNCTION RANDOM * 10000000
DISPLAY ELT-VALUE(POS)
END-PERFORM

* Sorting the array with Bubble Sort algorithm
PERFORM WITH TEST AFTER
VARYING I FROM ARRAY-SIZE BY -1 UNTIL I=2
AFTER J FROM 1 BY 1 UNTIL J = I - 1

COMPUTE J-PLUS1 = J + 1
* Swapping if needed
IF ELT-VALUE(J-PLUS1) < ELT-VALUE(J)
MOVE ELT-VALUE(J-PLUS1) TO ELT-VALUE-TEMP
MOVE ELT-VALUE(J) TO ELT-VALUE(J-PLUS1)
MOVE ELT-VALUE-TEMP TO ELT-VALUE(J)
END-IF
END-PERFORM

PERFORM VARYING POS FROM 1 BY 1 UNTIL POS > ARRAY-SIZE
DISPLAY ELT-VALUE(POS)
END-PERFORM

STOP RUN.
END PROGRAM BBUBSORT.

Laisser un commentaire Annuler la réponse